Подобие треугольников. Средняя линия треугольника
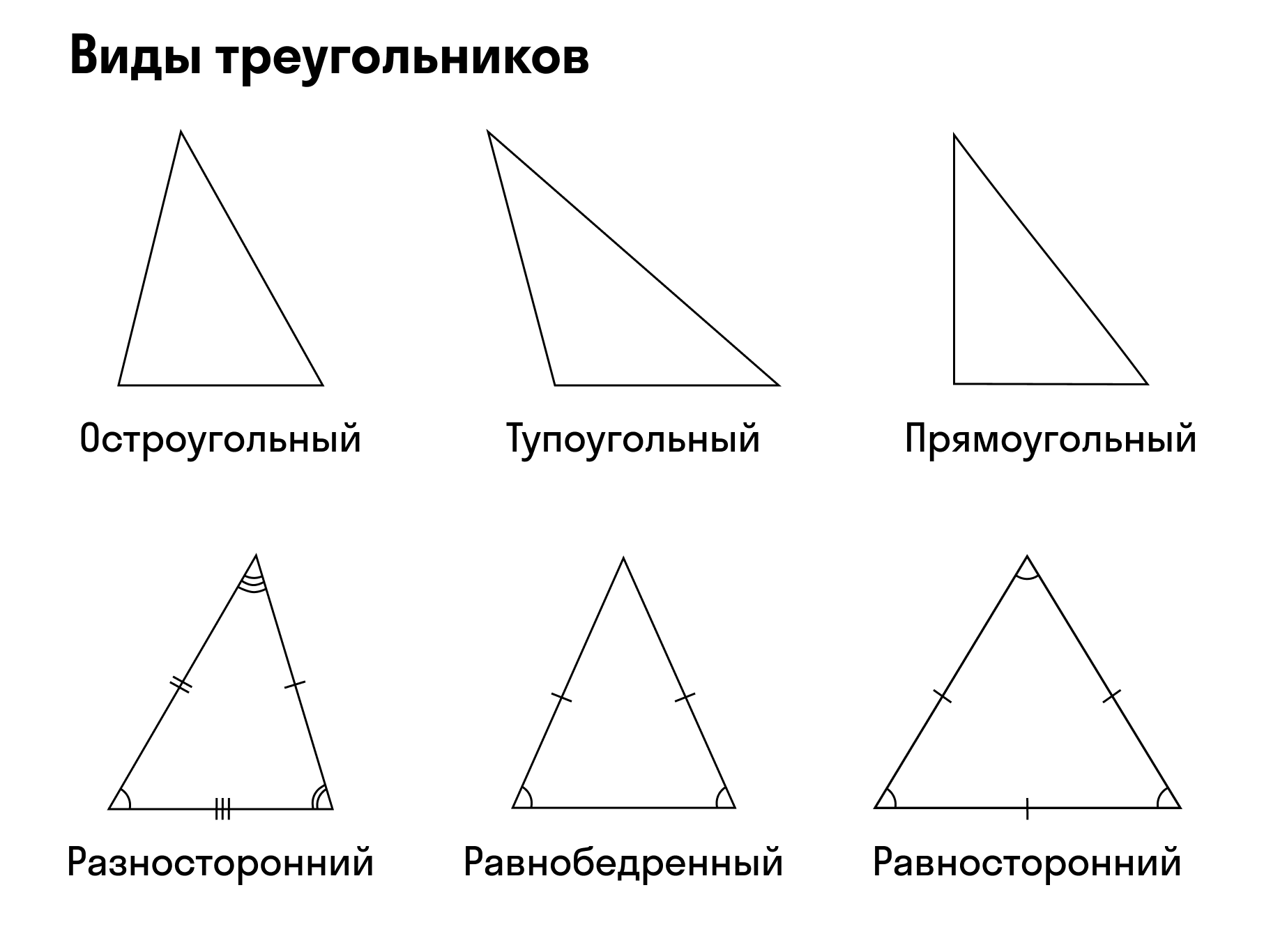
Треугольником называется фигура, которая состоит из трехточек, не лежащих на одной прямой, и трех отрезков, соединяющих этиточки попарно. Точки называются вершинами , а отрезки - сторонами треугольника. Треугольник называется разносторонним , если любые две стороны его не равны друг другу. Треугольник называется равнобедренным , если у него две стороны равны. Эти стороны называются боковыми, а третья сторона - основанием. Треугольник, все стороны которого равны, называется равносторонним.

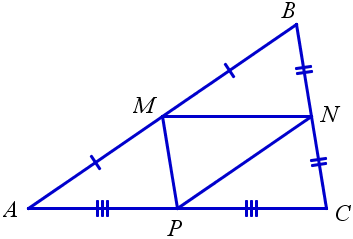
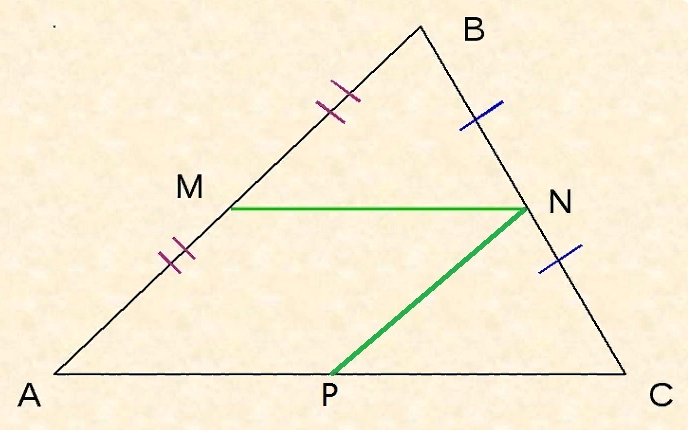


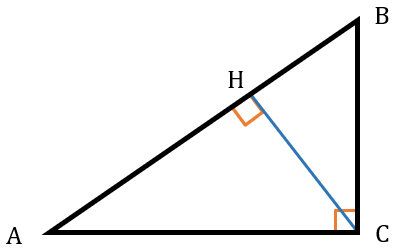


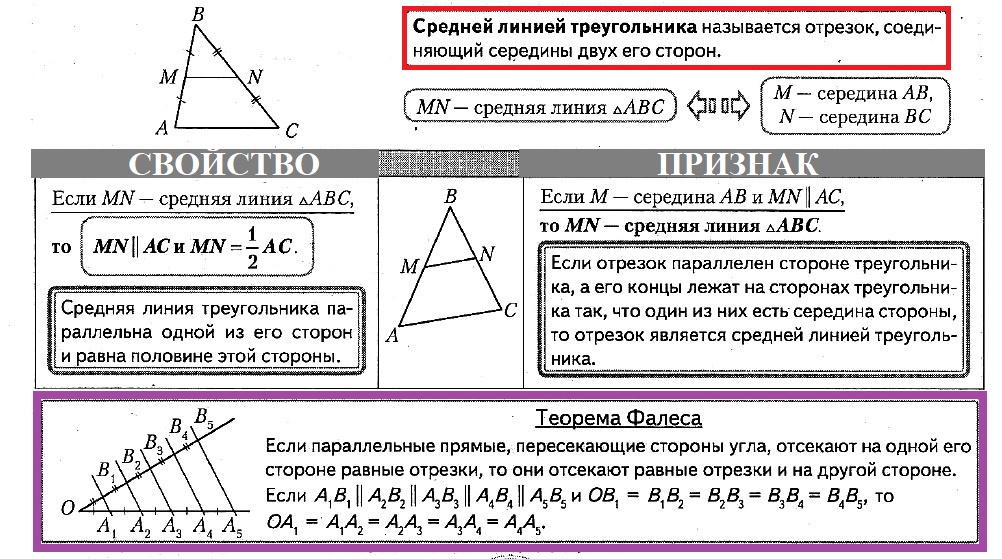
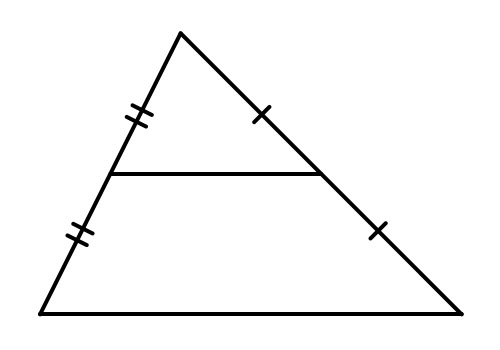
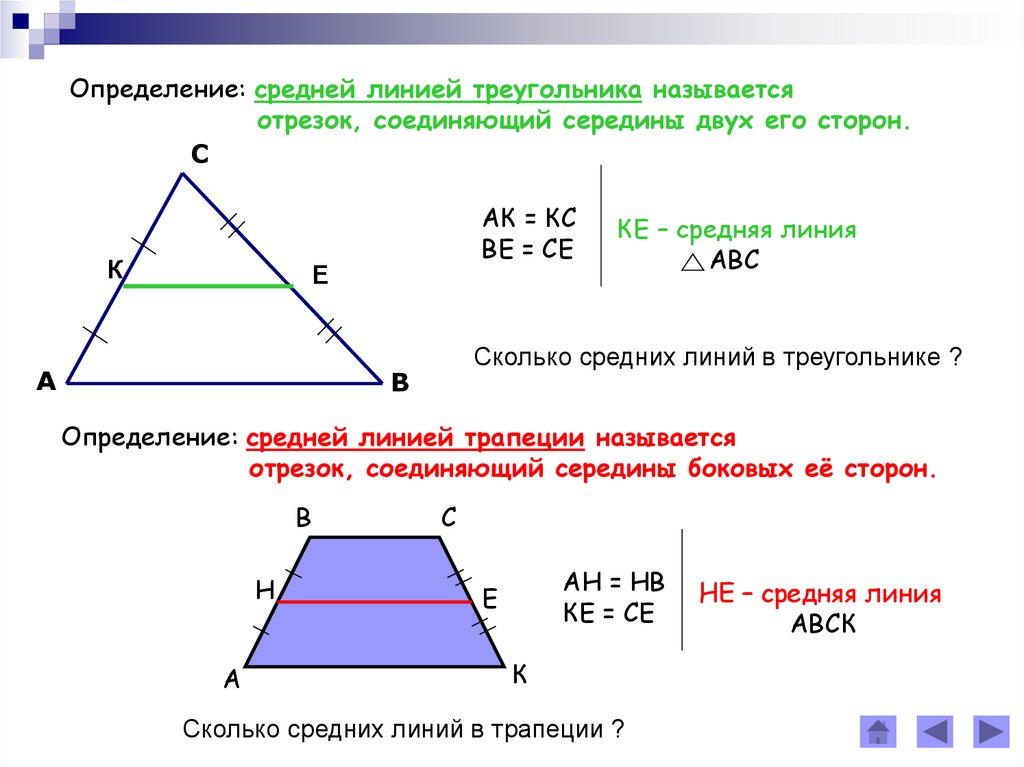
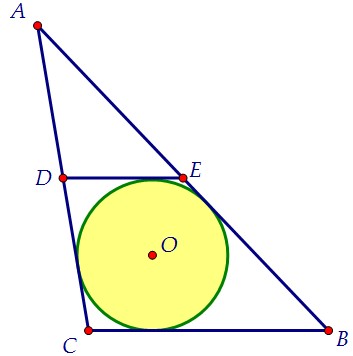
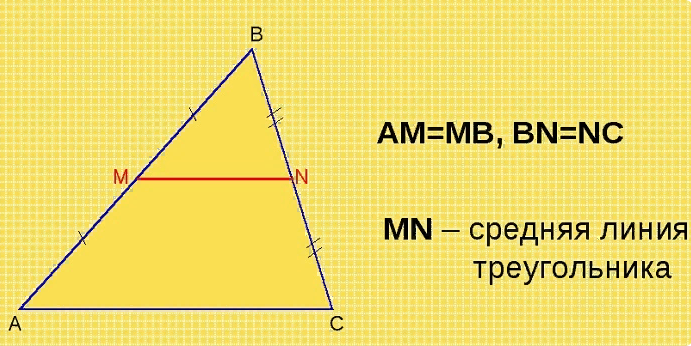
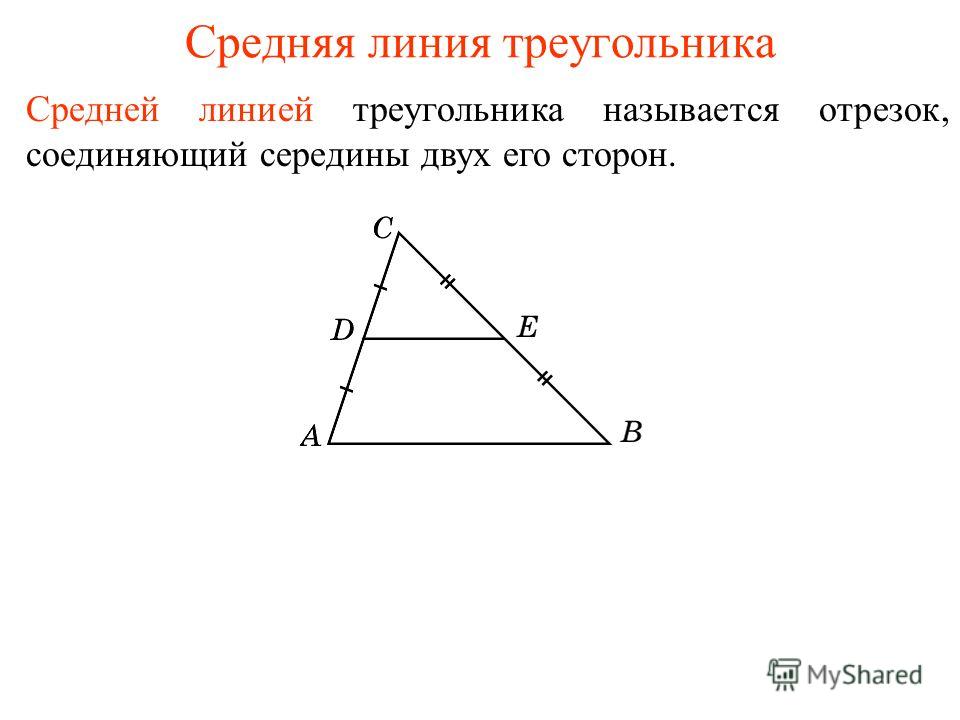
В данной публикации мы рассмотрим определение, свойства и признак средней линии треугольника, а также разберем пример решения задачи для лучшего понимания теоретического материала. Отрезок, который соединяет середины двух сторон треугольника, называется его средней линией. Средняя линия треугольника параллельна одной из его сторон которую не пересекает и в два раза меньше этой стороны. Средняя линия треугольника отсекает от него подобный треугольник в соотношении , площадь которого в 4 раза меньше исходного. Отрезок, проходящий через середину одной из сторон треугольника, пресекающий вторую и параллельный третьей стороне, является средней линией этого треугольника. Дан треугольник, две стороны которого равны 6 и 8 см.





Вместе с экспертом выясняем, что такое средняя линия треугольника, для чего она нужна и как это поможет в нахождении площади и периметра треугольника. Среднюю линию треугольника изучают на уроках геометрии в 8 классе, позже эта тема встречается в заданиях ЕГЭ по математике. Для решения экзаменационных задач ребятам нужно знать свойства и теорему средней линии, а также уметь вычислять через нее площадь и периметр треугольника. Вместе с экспертом-математиком разбираемся на примерах, как это правильно делать.