Раскраска графа
Работа выполнена на кафедре высшей математики факультета прикладной матсматики-процессов управления Санкт-Петербургского государственного университета. Защита состоится " ШЛ. С диссертацией можно ознакомиться в научной библиотеке им. Горького Санкт-Петербургского государственного университета по адресу: , Санкт-Петербург, Университетская наб. Актуальность работы.







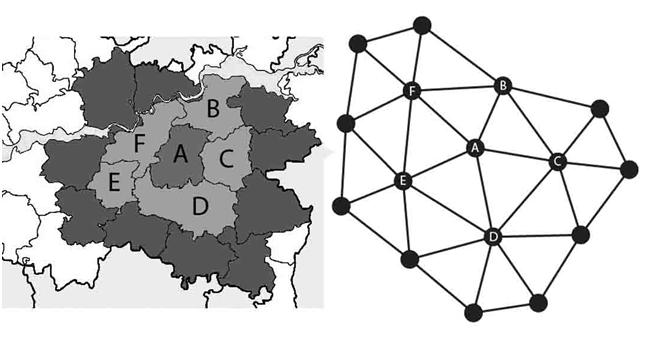
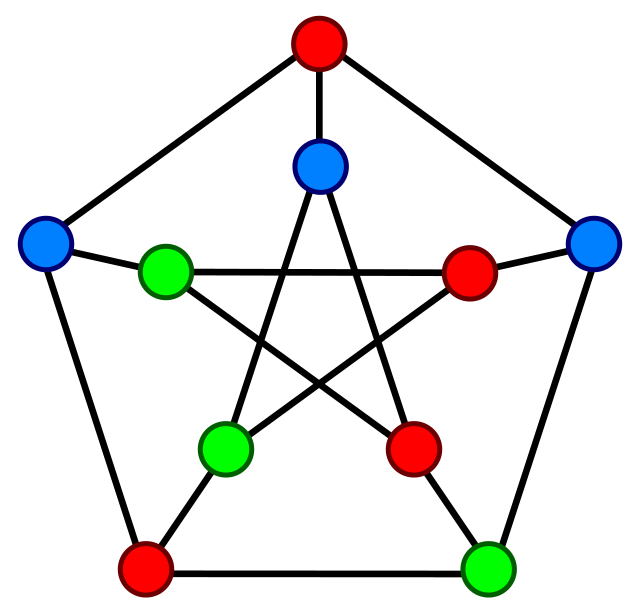
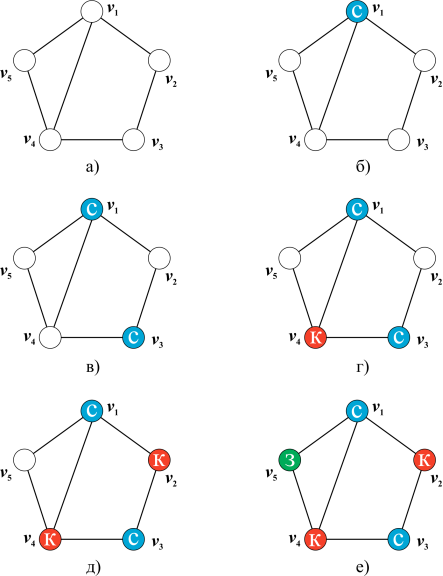
Раскраска графов - это теоретико-графовая конструкция, которая находит применение как в теоретических задачах, так и в практических областях, включая составление расписаний с ограничениями. Правильная раскраска графа регулярная раскраска представляет собой отображение множества вершин в множество цветов, удовлетворяющее условию разности цветов смежных вершин. В данной области активно исследуются и разрабатываются алгоритмы раскраски графов.
- Независимое множество вершин S внутреннее устойчивое подмножество - это такое подмножество вершин, в котором ни одна из вершин несмежная с любой другой вершиной данного множества.
- Раскраска графа Раскраска вершин графа. Раскраска графа Здравствуйте!
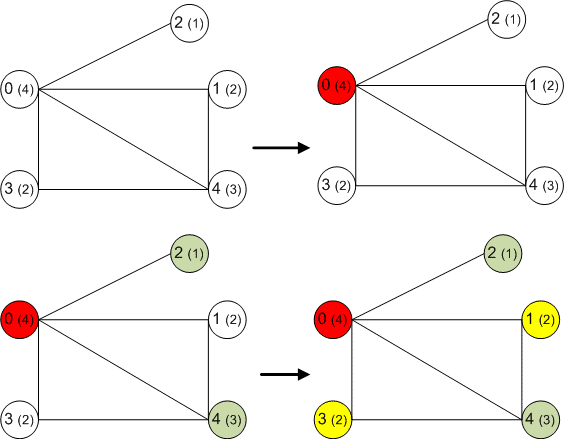
- При решении практических задач с применением графов возникает необходимость в разбиении множества вершин графа на классы попарно несмежных между вершин.

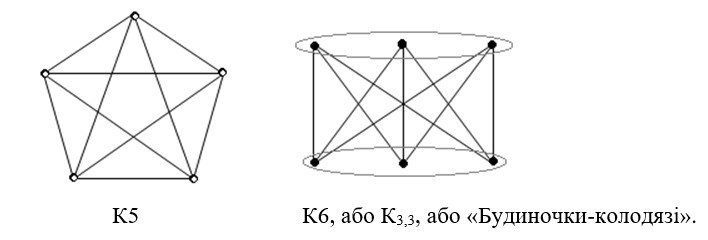



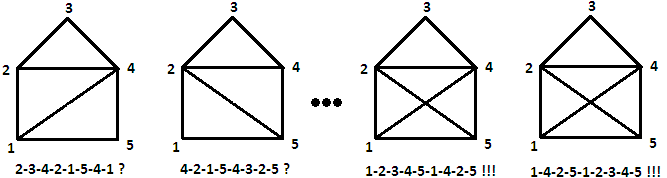
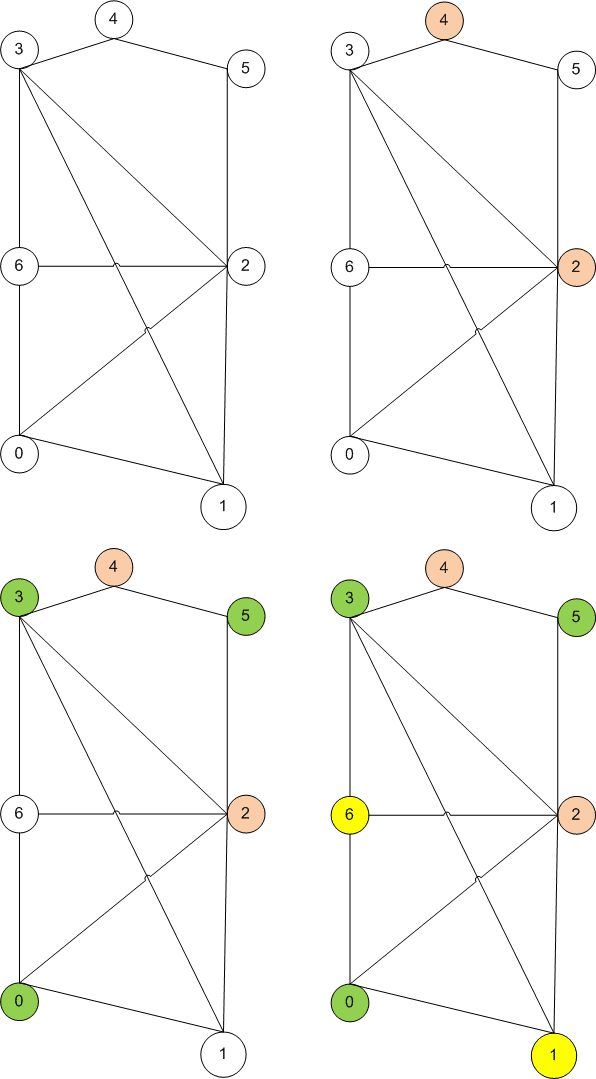
Так как граф является двудольным тогда и только тогда, когда все циклы четны, определить двудольность можно за один проход в глубину. На каждом шаге обхода в глубину помечаем вершину. Произведём серию поисков в ширину. Ту вершину, из которой мы начинаем идти, мы помещаем в первую долю. В процессе поиска в ширину, если мы идём в какую-то новую вершину, то мы помещаем её в долю, отличную от доли текущей вершину. Если же мы пытаемся пройти по ребру в вершину, которая уже посещена, то мы проверяем, чтобы эта вершина и текущая вершина находились в разных долях.